| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 평가지표
- ubuntu
- ml
- kernel
- FSL
- procedure
- pm2
- CT
- https
- error
- Dual energy X-ray
- object detection
- 동차좌표계
- git
- pytorch
- nodejs
- Cost Function
- Anaconda
- Emoji
- x-ray
- Homogeneous Coordinates
- Map-reduce
- coursera
- MySQL
- MRI
- NRMSE
- EC2
- AWS
- ssl
- relaxation time
- Today
- Total
Pay it Forward
[X-ray] X-ray 기초_4. X-ray 측정 및 이미징 (X-ray imaging, attenuation, beer-lambert law, intensity) 본문
[X-ray] X-ray 기초_4. X-ray 측정 및 이미징 (X-ray imaging, attenuation, beer-lambert law, intensity)
minjoony 2021. 11. 22. 20:31이번 게시글에서는 지난 게시글에서 살펴본 작용으로 감쇠된 X-ray의 strength(=intensity)를 측정하는 방식에 대하여 알아보고, 이를 이용하여 어떻게 imaging을 할 수 있는지 살펴보겠습니다.
X-ray imaging
지난게시글을 간단히 정리해보면,
X-ray는 물체와 부딪히면, 일부는 흡수(absortion)되고, 일부는 산란(scattering)됩니다.
중요한 것은 이 때! 에너지가 줄어든다(attenuation)는 것인데요!
X-ray가 부딪히는 물질에 따라 물질에 따라 attenuation정도가 다르다는 특징을 이용하여 imaging을 하게 됩니다.
Imaging과정과 메커니즘은 다음과 같습니다.
1. X-ray source에서 X-ray를 발생시키고,
2. 발생한 X-ray가 물체를 지나면서 감쇠하는데,
3. 물체를 이루는 각 물질에 따라 감쇠하는 정도가 다르므로 (즉, 통과하고 남은 X-ray의 strength가 다르므로)
4. Receptor(혹은 detector)에 닿게되는 X-ray strength를 측정하면 물질을 구분할 수 있다!

즉, receptor가 X-ray beam의 strength를 측정하여 imaging하는데
X-ray beam의 strength는 각 tissue에서의 attenuation정도에 따라 달라지므로 contrast가 발생하고
이를 imaging한 것이, 저희가 알고있는 X-ray image를 촬영하는 원리입니다.
X-ray intensity 측정
위에서 X-ray imaging을 하기 위해서는 X-ray beam의 strength를 측정해야 한다고 하였습니다.
X-ray beam의 strength를 intensity라고 합니다.
우선은, 물체에 의하여 감쇠(attenuation)가 되지 않은 경우.
즉, 허공에 X-ray를 쏘고 이를 receptor로 측정하는 경우에 대하여 먼저 살펴보겠습니다.
먼저, intensity는 receptor의 도달하는 X-ray photon의 개수($N$)에 비례할 것입니다.
따라서 우선 photon fluence($\Phi$)에 대한 수식을 먼저 세운다면 다음과 같습니다.
$ \Phi = {N} $
하지만 위의 수식은 얼만큼의 면적에 대한 photon의 개수인지를 나타내지 못하므로,
단위면적에서의 값을 측정하기 위하여 다음과 같이 unit area($A$)로 나눠줍니다.
$ \Phi = \frac{N}{A} $
추가로 x-ray beam의 측정시간이 $ \Delta t $일 경우에 단위시간당 intensity를 측정하고자 측정시간으로 나눠줍니다.
$ \Phi = \frac{N}{A\Delta t} $
자, 이렇게 위의 수식은 X-ray photon의 단위면적, 단위시간에서의 양을 나타내게 되었습니다.
이 값에 photon 1개당 가지고 있는 energy($E$)를 곱해주면,
저희가 구하고자 하는 intensity($I$)를 다음과 같이 구할 수 있습니다.
$ I = E \Phi = \frac{EN}{A\Delta t} $
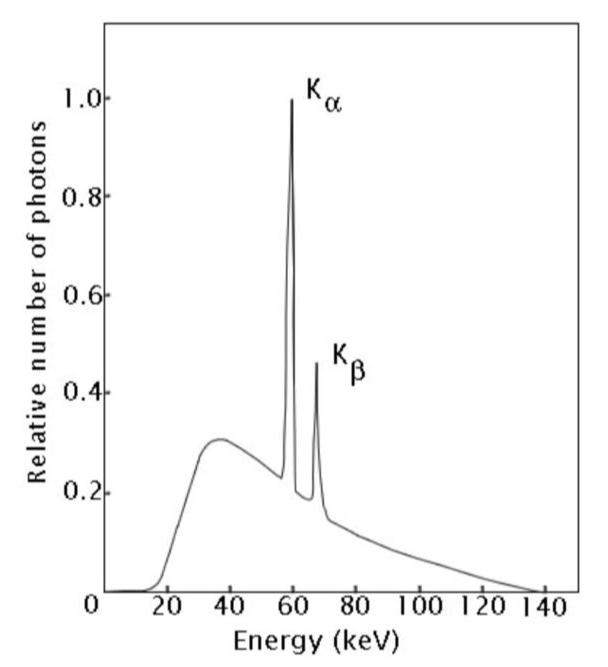
위 그래프는 이전에 bremsstrahlung X-ray, characteristic X-ray를 살펴볼 때 보았던 그래프입니다.
y축이 photon의 개수를 의미하고, x축이 각 photon의 unit energy를 의미합니다.
따라서 위 그래프를 $S(E)$라고 한다면, 총 photon fluence rate은 다음과 같이 $S(E)$의 적분으로 나타낼 수 있습니다.
$ \Phi = \int_{0}^{\infty} S(E), dE $
마찬가지로, intensity는 photon fluence rate에 각 photon의 energy를 곱한값의 적분으로 나타낼 수 있습니다.
$ I = \int_{0}^{\infty} E*S(E), dE $
자, 여기까지 저희는 허공에 X-ray beam을 쏘고,
receptor를 통해 X-ray beam의 intensity를 측정하는 과정을 보았습니다.
이제는 물체가 있을 때의 상황을 살펴보겠습니다.
아래 그림과 같이 $\Delta x$의 두께(thickness)를 갖는 물체가 있고,
X-ray beam이 X-ray source로부터 직선으로 와서 receptor에 직선으로 꽂힌다고 가정해봅시다.
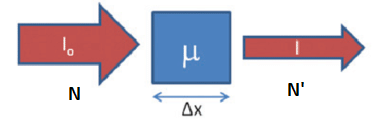
이 때, X-ray source로부터 나온 X-ray photon의 개수가 $N$개,
물체를 지나면서 감소되어 receptor에 닿은 X-ray photon의 개수를 $N'$이라고 한다면
물체에 의해서 잃은 photon의 개수($n$)는 다음과 같이 $N$과 물체의 두께에 비례할 것입니다.
(Source로부터 나온 photon이 많을수록 잃게되는 photon도 많아지고, 물체가 두꺼울수록 잃는 photon이 많아지기 때문이죠)
$ n = N - N' = \mu N \Delta x $
여기에서 $\mu$는 linear attenuation coeeficient라고 하며,
앞서 물체마다 photon의 양을 감소시키는 정도가 다르다고 하였는데 그것을 지칭하는 물질 dependent한 상수입니다.
아래와 같이 식을 다시 써보면, 물체의 단위길이(unit length)에 대한 photon의 감쇠정도를 나타내는 것을 알 수 있습니다.
$ \mu = \frac {n/N} {\Delta x} $
다시, 본론으로 돌아와서, photon의 개수에 대한 변화량($\Delta N$)은 다음과 같이 나타낼 수 있습니다.
$ \Delta N = N' - N = -n = -\mu N \Delta x $
위 식을 $N$에 대하여 미분하면 다음과 같습니다.
$ \frac {dN} {N} = -\mu \Delta x dx $
이 미분방정식을 풀면, 아래와 같이 수식을 이끌어낼 수 있고, 이를 fundamental photon attenuation law라고 합니다.
($N$ = thickness가 0일 때의 photon 개수. 즉, 물체가 없는 경우의 photon 개수이자 source에서 나온 photon 개수)
$ N' = N e^{-\mu \Delta x} $
마찬가지로 intensity에 대한 수식도 다음과 같이 나타낼 수 있으며,
이 식은 Beer-Lambert law라고도 불립니다.
$ I' = I e^{-\mu \Delta x} $
만약, 물체의 부위마다 다른 물질로 이루어져 있다면 (= inhomogeneous)
각 부위마다 $\mu$가 다를테고, 이를 $\mu(x)$로 나타낼 수 있습니다.
따라서 물체를 이루는 물질이 다른 경우는 다음과 같이 수식이 변하게 됩니다.
$ N(x) = N_0 e^{-\int_{0}^{x} \mu(x'), dx'} $
$ I(x) = I_0 e^{-\int_{0}^{x} \mu(x'), dx'} $
이제 마지막으로, X-ray photon마다 다양한 energy를 가진다고 하였고, 위의 그래프($S(E)$)로 나타냈었습니다.
각 photon의 energy를 반영하면 다음과 같이 최종적으로 수식을 나타낼 수 있습니다.
$ S(x; E) = S_0(E) e^{-\int_{0}^{x} \mu(x'; E), dx'} $
$ I(x) = \int_{0}^{\infty} S_0(E')E' e^{-\int_{0}^{x} \mu(x'; E), dx'} dE' $
(intensity는 $photon$ $number * photon$ $energy$ 이므로 수식에 $E'$가 곱해졌음에 유의합니다.)
References
Jerry L. Prince, Jonathan M.Links 『Medical imaging signals and systems』, Pearson (2006)




