| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- FSL
- 평가지표
- MySQL
- CT
- relaxation time
- pytorch
- pm2
- procedure
- ubuntu
- Dual energy X-ray
- nodejs
- Cost Function
- MRI
- ml
- Anaconda
- Emoji
- x-ray
- Homogeneous Coordinates
- coursera
- git
- NRMSE
- 동차좌표계
- ssl
- kernel
- Map-reduce
- EC2
- error
- object detection
- AWS
- https
- Today
- Total
Pay it Forward
[MRI] MRI 원리_ch2. Preliminaries 본문
** 본 글은 Principles of Magnetic Resonance Imaging (Dwight G. Nishimura)의 책을 공부한 게시글입니다.
Chapter 2. Preliminaries
해당 챕터에서는 MRI의 원리를 이해하기 위한 수학, 신호 사전지식을 소개하고 있다.
2.1 Complex Numbers
복소수 c는 다음과 같이 실수부(real)와 허수부(imaginary)로 나눌 수 있다.
$ c = a + ib $
이를 직각좌표 형식으로 나타내었다고 하며, $i = \sqrt{-1}$, $a$는 실수부, $b$는 허수부를 의미한다.
이러한 복소수 c는 다음과 같이 지수 형식으로도 나타낼 수도 있다.
$ c = Ae^{i\phi} = A(\cos\phi + i\sin\phi)$
$A$는 magnitude(진폭), $\phi$는 phase(위상)을 나타내며,
직각좌표 형식으로 나타냈을때의 실수부($a$), 허수부($b$)와의 관계는 다음과 같다.
$A = \sqrt{a^2 + b^2}$
$\phi = \tan^{-1}\frac{b}{a}$
또한, $\phi$가 시간에 따라 linear하게 변한다면, 다음과 같이 나타낼 수 있다.
$\phi = \omega t (rad/s) = 2\pi ft (Hz)$
이 때, $A$는 vector의 길이(length)를, $\phi$는 vector의 방향(direction)와 관련이 있다.

위와 같이 복소수를 복소좌표에 나타내어 복소수에 해당하는 vector를 표현할 수 있다.
(복소좌표란 x축이 실수부, y축이 허수부를 나타내는 직각좌표평면이다.)
주로 다음과 같이 t에 대한 함수로서 복소수를 벡터로 표현한다. (time-varying vector)
$c(t) = Ae^{i(-\omega)t + i\phi_0} = Ae^{-i\omega t}e^{i\phi_0}$
$\phi_0$는 starting phase이고, $\omega$는 각 주파수를 의미한다.
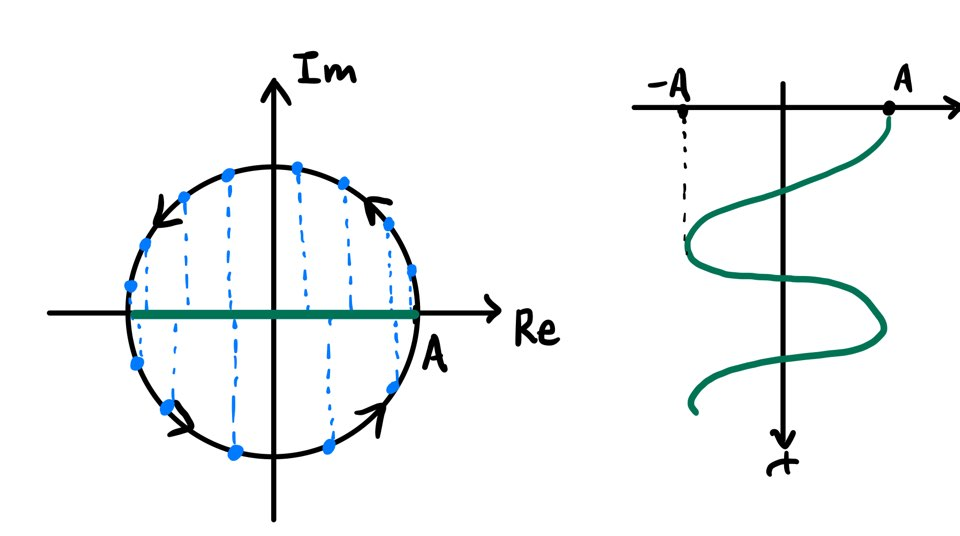
즉, 위와 같은 함수를 통해 $t$에 따라 벡터가 시계방향으로 도는것을 알 수 있다. (clockwise rotation)
이 때, $A$는 rotation을 하는 원의 크기(반지름)와 관련이 있고, $\omega$는 rotation하는 속도와 관련이 있다.
오일러 정리를 통해 다음과 같이 나타낼 수 있으며, $Acos {(\omega t)}$는 실수부, $-Asin {(\omega t)}$는 허수부이다.
이러한 사실은 다음 그림과 같이 rotation을 각 축으로 projection 시켜보면 알 수 있다.
$Ae^{-i\omega t} = A\cos {(\omega t)} - A\sin {(\omega t)}$
2.2 Fourier Transforms
'Bio, Medical > MRI' 카테고리의 다른 글
| [MRI] MRI 기초_2. 주요 자기장(B0, B1, G)과 주요 physics(polarization, excitation, relaxation) (0) | 2021.09.15 |
|---|---|
| [MRI] MRI 원리_ch1. Introduction (0) | 2020.12.21 |
| [MRI] MRI 기초_3. T1, T2 relaxation time과 weighted image (4) | 2020.12.08 |
| [MRI] MRI 기초_1. 기본 원리 (1) | 2020.11.26 |




