[평가지표] ROC curve와 AUC
ROC curve (Receiver Operating Characteristic curve)
ROC curve는 classification에서 자주 사용되는 evaluation metric이다. (엄밀히 말하면 AUC가 자주 사용된다.)
항상 직관적으로 줄임말의 어원을 통해 해당 단어의 성질을 파악하고자 노력하는데, ROC는 잘 파악이 안된다.
그래도 막무가내로 파악을 해보자면..
병이 있다고(Positive) 혹은 없다고(Negative) 판단을 하였을때, receiver가 어떻게 판단하여 작동할지를 표시해 놓은 curve... 가 될지 모르겠다. 괜히 직관적으로 이해해보려 한걸지도 ^^;
쨋든, ROC는 Sensitivity와 Specificity의 관계를 그래프(curve)로 나타낸 것이다.
(Sensitivity와 Specificity를 모른다면 다음 게시글을 참고하자.)
사실 거짓말이다.
TPR과 FPR (= 1-specificity)을 그래프로 나타낸것이다. (의미는 같다)
왜 Sensitivity와 Specificity를 그래프로 나타내지 않고 굳이 TPR과 FPR로 나타냈을까?
TPR과 FPR을 그래프로 나타낸 것보다 Sensitivity와 Specificity를 그래프로 나타낸 것이 우상향 그래프로,
우리에게 더욱 익숙하고 읽기 쉽기 때문이다.

AUC (Area Under the Curve)
AUC는 ROC curve의 곡선 아래 영역을 나타내며 classification 성능평가지표로 많이 사용된다.
1에 가까울수록 성능이 우수하다고 판단하며
0.5인 경우에 최악의 성능이다. (이는 model이 classification 능력이 없음을 의미한다.)
만약 AUC값이 0.5 미만이라면 Labeling 혹은 Algorithm이 잘못됐을 가능성이 크다.
(stats.stackexchange.com/questions/266387/can-auc-roc-be-between-0-0-5)

임상(clinical)에서 사용할 수 있을 정도의 모델이라면 AUC가 적어도 0.8 이상은 나와야 한다.

AUC에 대해 좀 더 고찰해보면,
Sensitivity와 Specificity가 결국은 확률(Probability)에 관한 것이므로 다음 그림과 같이 확률분포로 나타낼 수 있다.
(녹색 : 병에 걸리지 않은 경우, 적색 : 병에 걸린 경우를 의미한다.)
Threshold값에 따라서 FP, FN 등이 변하게 되는데,
threshold를 최대한 낮게 잡는 경우 (모든 환자에게 병에 걸렸다고 하는 경우)는 2번째 그림에서의 a와 같다.
이 경우에는 FPR과 TPR이 모두 1값을 갖는다.
반대로 threshold를 최대한 높게 잡는 경우 (모든 환자에게 병에 걸리지 않았다고 하는 경우)는 b와 같다.
이 경우에는 FPR와 TPR이 모두 0값을 갖는다.
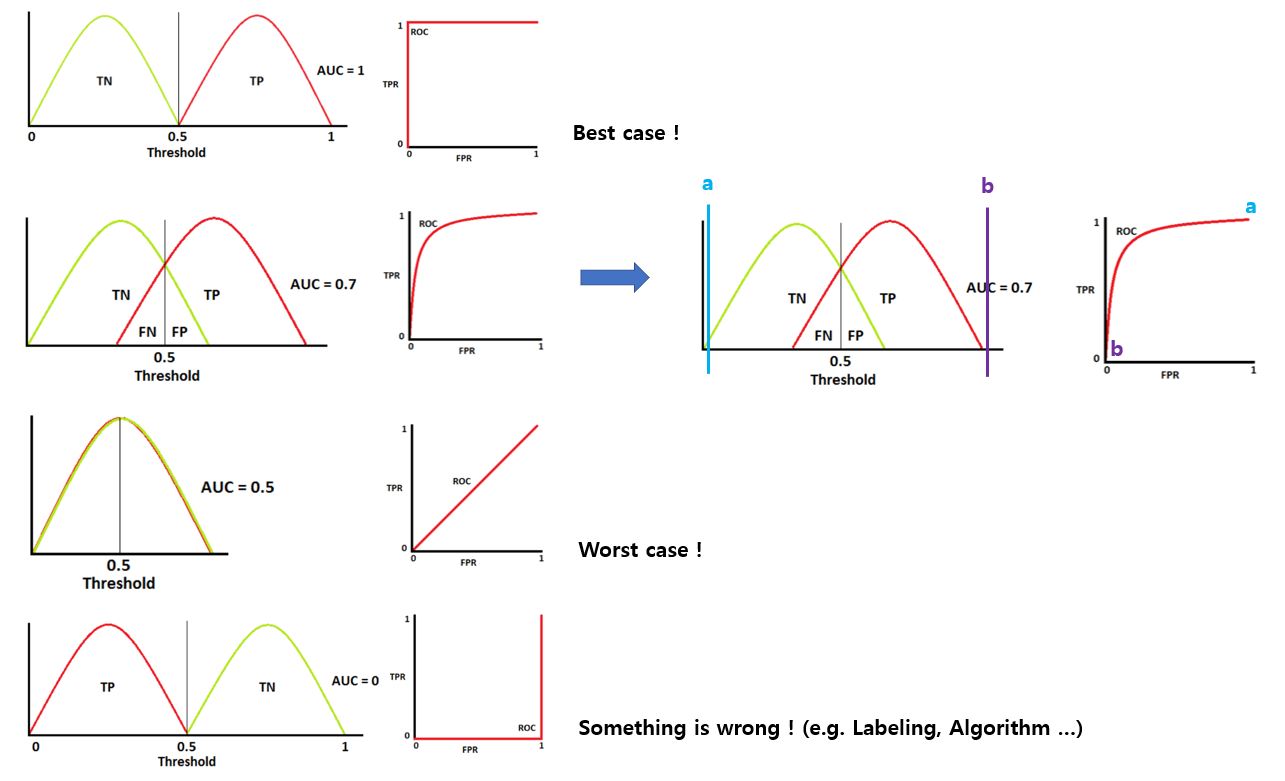
AUC에 대한 설명은 마치고, AUC를 통해 어떻게 classification model을 평가하는지에 대해 좀 더 서술해보자면,
보통 딥러닝 모델은 classification을 수행하기 위하여 image의 특징을 학습한다.
이 때, classification을 잘 수행하기 위해서는 위 그림의 첫번째 그림과 같이,
각 image들이 최대한 분리될수있는(separable) 대표적 특징들을(feature representation) 학습하는 것이 관건이다.
즉, AUC가 높게 산출되도록 separable한 feature를 학습한 모델이 classification에서의 성능이 우수하다고 판단할 수 있는 것이다.
따라서 AUC가 높은 모델은 classification에 있어서 각 case를 잘 분리할 수 있는 feature를 학습한 모델이라고 볼 수 있다.
+a) Sensitivity (민감도), Specificity (특이도)
Sensitivity = True Positive Rate (병이 실제로 있고, 이를 맞춘 경우)
Specificity = True Negative Rate (병이 실제로 없고, 이를 맞춘 경우) = 1 - FPR

TPR와 FPR은 비례관계에 있다.
만약 어떤 의사가 모든 환자에 대하여 병이 있다고 진단한다면 TPR과 FPR이 모두 올라갈 것이다.
(위의 수식을 보면 당연하다.)
그러나, Sensitivity와 Specificity는 반비례관계에 있다.